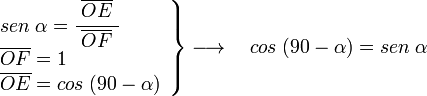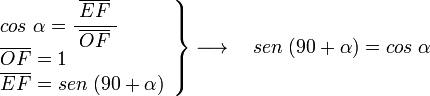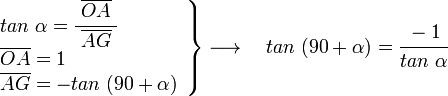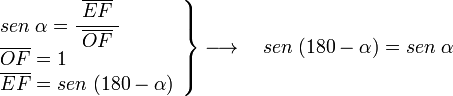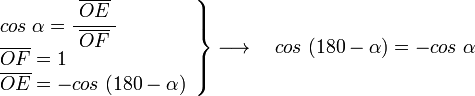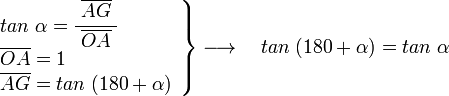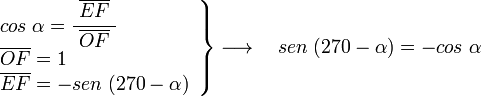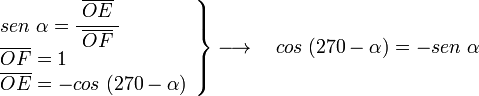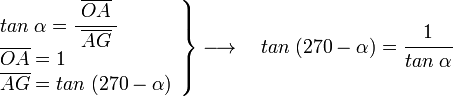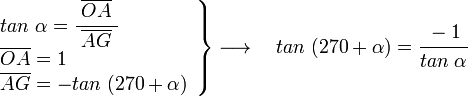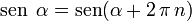sábado, 28 de julio de 2012
viernes, 27 de julio de 2012
calcullo de algunos casos
Cálculo de algunos casos
Partiendo
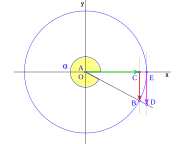
de una circunferencia de radio uno, dividida en cuatro cuadrantes, por
dos rectas perpendiculares, que se cortan en el centro de la
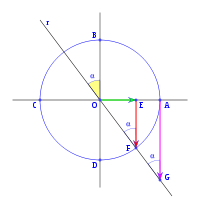
circunferencia O, estas rectas cortan a la circunferencia en los puntos A, B, C y D, la recta horizonte AC también la podemos llamar eje x y la recta vertical BD eje y. Dada una recta r, que pasa por el centro de la circunferencia y forma un ángulo α con OA, eje x, y corta a la circunferencia en F, tenemos que la vertical que pasa por F corta al eje x en E, la vertical que pasa por A corta a la recta r en G. Con todo esto definimos, como ya se vio anteriormente, las funciones trigonométricas:
para el seno:
dado que:
Para el coseno:
dado que:
Para la tangente:
dado que:
partiendo de estas definiciones, podemos ver algunos caso importantes:
[editar]Para 90-α
Si a partir del eje vertical OB trazamos la recta r a un ángulo α en el sentido horario, la recta r forma con el eje x un ángulo 90-α, el valor de las funciones trigonométricas de este ángulo conocidas las de α serán:
El triángulo OEF rectángulo en E, siendo el ángulo en F α, por lo tanto:
en el mismo triángulo OEF, tenemos que:
viendo el triángulo OAG, rectángulo en A, siendo el ángulo en G igual a α, podemos ver:
[editar]Para 90+α
Si a partir de eje vertical OB trazamos la recta r a un ángulo α, medido en sentido trigonométrico, el ángulo formado por el eje horizontal OA y la recta r será 90+α. La prolongación de la recta r corta a la circunferencia en F y a la vertical que pasa por A en G.
El triángulo OEF es rectángulo en E y su ángulo en F es α, por lo tanto tenemos que:
En el mismo triángulo OEF podemos ver:
En el triángulos OAG rectángulo A y siendo α el ángulo en G, tenemos:
[editar]Para 180-α
Si sobre el eje horizontal OC, trazamos la recta r a un ángulo α, el ángulo entre el eje OA y la recta r es de 180-α, dado el triángulo OEF rectángulo en E y cuyo ángulo enO es α, tenemos:
en el mismo triángulo OEF:
En el triángulo OAG, rectángulo en A y con ángulo en O igual a α, tenemos:
[editar]Para 180+α
Sobre la circunferencia de radio uno, a partir del eje OC con un ángulo α trazados la recta r, el ángulo del eje OA y la recta r es de 180+α, como se ve en la figura. En el triángulo OEF rectángulo en E se puede deducir:
en el mismo triángulo OEF tenemos:
en el triángulo OAG, rectángulo en A, vemos que:
[editar]Para 270-α
Sobre el eje OD y con un ángulo α medido en sentido horario trazamos la recta r. El ángulo entre el eje OA y la recta r es de 270-α. En el triángulo OEF, rectángulo en E, tenemos:
por otra parte en el mismo triángulo OEF, tenemos:
en el triángulo OAG rectángulo en A, y siendo α el ángulo en G, tenemos;
[editar]Para 270+α
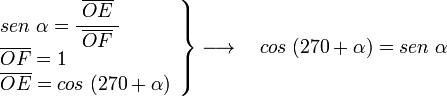
Sobre el eje OD y con un ángulo α medido en sentido trigonométrico, trazamos la recta r. El ángulo entre el eje OA y la recta r es de 270+α. En el triángulo OEF, rectángulo en E, tenemos:
por otra parte en el mismo triángulo OEF, tenemos:
en el triángulo OAG rectángulo en A, y siendo α el ángulo en G, tenemos;
[editar]
Para -α
Sobre la circunferencia de radio uno, a partir del eje OA con un ángulo α medido en sentido horario trazados la recta r, el ángulo del eje OA y la recta r es de -α, o lo que es lo mismo 360-α como se ve en la figura. En el triángulo OEF rectángulo en E se puede deducir:

en el mismo triángulo OEF tenemos:

en el triángulo OAG, rectángulo en A, vemos que:




cuarto cuadrante
Cuarto cuadrante
En el cuarto cuadrante, que comprende los valores del ángulo  entre
entre  rad y
rad y  rad, las variables trigonométricas varían desde los valores que toman para
rad, las variables trigonométricas varían desde los valores que toman para  rad:
rad:
 entre
entre  rad y
rad y  rad, las variables trigonométricas varían desde los valores que toman para
rad, las variables trigonométricas varían desde los valores que toman para  rad:
rad:
hasta los que toman para  rad pasando al primer cuadrante, completando una rotación:
rad pasando al primer cuadrante, completando una rotación:
 rad pasando al primer cuadrante, completando una rotación:
rad pasando al primer cuadrante, completando una rotación:


- como puede verse a medida que el ángulo
 aumenta, aumenta el coseno
aumenta, aumenta el coseno 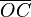 en el lado positivo de las x, el seno
en el lado positivo de las x, el seno  disminuye en el lado negativo de las y, y la tangente
disminuye en el lado negativo de las y, y la tangente  también disminuye en el lado negativo de las y.Cuando
también disminuye en el lado negativo de las y.Cuando , vale
, vale  ó
ó  al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.Dado el carácter rotativo de las funciones trigonométricas, se puede afirmar en todos los casos:Que cualquier función trigonométrica toma el mismo valor si se incrementa el ángulo un número entero de rotaciones completas.
al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.Dado el carácter rotativo de las funciones trigonométricas, se puede afirmar en todos los casos:Que cualquier función trigonométrica toma el mismo valor si se incrementa el ángulo un número entero de rotaciones completas.
Suscribirse a:
Entradas (Atom)