Sentido de las funciones trigonométricas
Dados los ejes de coordenadas cartesianas xy, de centro O, y una circunferencia goniométrica (circunferencia de radio la unidad) con centro en O; el punto de corte de la circunferencia con el lado positivo de las x, lo señalamos como punto E.
Nótese que el punto A es el vértice del triángulo, y O es el centro de coordenada del sistema de referencia:
a todos los efectos.
La recta r, que pasa por O y forma un ángulo 
sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
Por semejanza de triángulos:
Los puntos E y B están en la circunferencia de centro O, por eso la distancia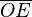 
y 
son
el radio de la circunferencia, en este caso al ser una circunferencia
de radio = 1, y dadas las definiciones de las funciones trigonométricas:
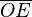y son
el radio de la circunferencia, en este caso al ser una circunferencia
de radio = 1, y dadas las definiciones de las funciones trigonométricas:
tenemos:
La tangente es la relación del seno entre el coseno, según la definición ya expuesta.
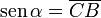
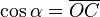
No hay comentarios:
Publicar un comentario