Segundo cuadrante
Cuando el ángulo  supera el ángulo recto, el valor del seno empieza a disminuir según el segmento
supera el ángulo recto, el valor del seno empieza a disminuir según el segmento  , el coseno aumenta según el segmento
, el coseno aumenta según el segmento 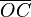 , pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
, pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
 supera el ángulo recto, el valor del seno empieza a disminuir según el segmento
supera el ángulo recto, el valor del seno empieza a disminuir según el segmento  , el coseno aumenta según el segmento
, el coseno aumenta según el segmento 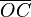 , pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
, pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
La tangente para un ángulo  inferior a
inferior a  rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los
rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los  rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente
rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente  por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo
por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo  aumenta progresivamente hasta los
aumenta progresivamente hasta los 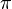 rad.
rad.
 inferior a
inferior a  rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los
rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los  rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente
rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente  por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo
por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo  aumenta progresivamente hasta los
aumenta progresivamente hasta los 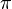 rad.
rad.
Resumiendo: en el segundo cuadrante el seno de  ,
,  , disminuye progresivamente su valor desde 1, que toma para
, disminuye progresivamente su valor desde 1, que toma para  rad, hasta que valga 0, para
rad, hasta que valga 0, para  rad, el coseno,
rad, el coseno,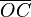 , toma valor negativo y su valor varia desde 0 para
, toma valor negativo y su valor varia desde 0 para  rad, hasta –1, para
rad, hasta –1, para  rad.
rad.
 ,
,  , disminuye progresivamente su valor desde 1, que toma para
, disminuye progresivamente su valor desde 1, que toma para  rad, hasta que valga 0, para
rad, hasta que valga 0, para  rad, el coseno,
rad, el coseno,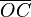 , toma valor negativo y su valor varia desde 0 para
, toma valor negativo y su valor varia desde 0 para  rad, hasta –1, para
rad, hasta –1, para  rad.
rad.
La tangente conserva la relación:
incluyendo el signo de estos valores.
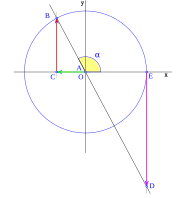
Para un ángulo llano tenemos que el punto D esta en E, y B y C coinciden en el eje de las x en el lado opuesto de E, con lo que tenemos:



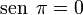

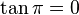
No hay comentarios:
Publicar un comentario