Cuarto cuadrante
En el cuarto cuadrante, que comprende los valores del ángulo  entre
entre  rad y
rad y  rad, las variables trigonométricas varían desde los valores que toman para
rad, las variables trigonométricas varían desde los valores que toman para  rad:
rad:
 entre
entre  rad y
rad y  rad, las variables trigonométricas varían desde los valores que toman para
rad, las variables trigonométricas varían desde los valores que toman para  rad:
rad:
hasta los que toman para  rad pasando al primer cuadrante, completando una rotación:
rad pasando al primer cuadrante, completando una rotación:
 rad pasando al primer cuadrante, completando una rotación:
rad pasando al primer cuadrante, completando una rotación:


- como puede verse a medida que el ángulo
 aumenta, aumenta el coseno
aumenta, aumenta el coseno  en el lado positivo de las x, el seno
en el lado positivo de las x, el seno  disminuye en el lado negativo de las y, y la tangente
disminuye en el lado negativo de las y, y la tangente  también disminuye en el lado negativo de las y.Cuando
también disminuye en el lado negativo de las y.Cuando , vale
, vale  ó
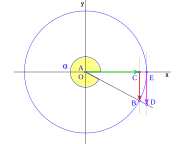
ó  al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.Dado el carácter rotativo de las funciones trigonométricas, se puede afirmar en todos los casos:Que cualquier función trigonométrica toma el mismo valor si se incrementa el ángulo un número entero de rotaciones completas.
al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.Dado el carácter rotativo de las funciones trigonométricas, se puede afirmar en todos los casos:Que cualquier función trigonométrica toma el mismo valor si se incrementa el ángulo un número entero de rotaciones completas.





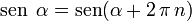

hayy mi amor jennifer que bonito trabajo.....
ResponderEliminar