Tercer cuadrante
En el tercer cuadrante, comprendido entre los valores del ángulo  rad a
rad a 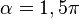 rad, se produce un cambio de los valores del seno, el coseno y la tangente, desde los que toman para
rad, se produce un cambio de los valores del seno, el coseno y la tangente, desde los que toman para 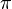 rad:
rad:
 rad a
rad a 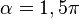 rad, se produce un cambio de los valores del seno, el coseno y la tangente, desde los que toman para
rad, se produce un cambio de los valores del seno, el coseno y la tangente, desde los que toman para 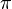 rad:
rad:
Cuando el ángulo  aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
 aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
A medida que el ángulo crece el punto C se acerca a O, y el segmento 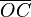 , el coseno, se hace más pequeño en el lado negativo de las x.
, el coseno, se hace más pequeño en el lado negativo de las x.
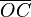 , el coseno, se hace más pequeño en el lado negativo de las x.
, el coseno, se hace más pequeño en el lado negativo de las x.
El punto B, intersección de la circunferencia y la vertical que pasa por C, se aleja del eje de las x, en el sentido negativo de las y, el seno,  .
.
 .
.
Y el punto D, intersección de la prolongación de la recta r y la vertical que pasa por E, se aleja del eje las x en el sentido positivo de las y, con lo que la tangente,  , aumenta igual que en el primer cuadrante
, aumenta igual que en el primer cuadrante
 , aumenta igual que en el primer cuadrante
, aumenta igual que en el primer cuadrante
Cuando el ángulo  alcance
alcance  rad, el punto C coincide con O y el coseno valdrá cero, el segmento
rad, el punto C coincide con O y el coseno valdrá cero, el segmento  será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
 alcance
alcance  rad, el punto C coincide con O y el coseno valdrá cero, el segmento
rad, el punto C coincide con O y el coseno valdrá cero, el segmento  será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
El seno el coseno y la tangente siguen conservando la misma relación:
que
se cumple tanto en valor como en signo, nótese que a medida que el
coseno se acerca a valores cercanos a cero, la tangente tiende a
infinito.







No hay comentarios:
Publicar un comentario